|
|
|
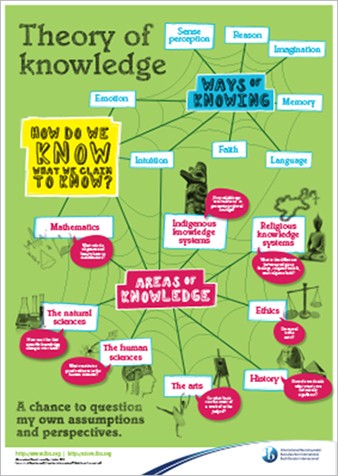
The sum of all positive integers...
|
|
|
|
60 Second Adventures in Thought
|
Theory of Knowledge by Mathematical Topic
Topic 1 - Algebra
TOK: Mathematics and the world. Some mathematical constants (pi, e, , Fibonacci numbers) appear consistently in nature. What does this tell us about mathematical knowledge?
TOK: Mathematics and the knower. How is mathematical intuition used as a basis for formal proof? (Gauss’ method for adding up
integers from 1 to 100.)
TOK: The nature of mathematics and science. Were logarithms an invention or discovery?
TOK: The nature of mathematics. The unforeseen links between Pascal’s triangle, counting methods and the coefficients of
polynomials. Is there an underlying truth that can be found linking these?
TOK: Mathematics and the knower. Do the words imaginary and complex make the concepts more difficult than if they had
different names?
TOK: The nature of mathematics. Has “i” been invented or was it discovered?
TOK: Mathematics and the world. Why does “i” appear in so many fundamental laws of physics?
TOK: The nature of mathematics. Was the complex plane already there before it was used to represent complex numbers
geometrically?
TOK: Mathematics and the knower. Why might it be said that e^ip + 1 = 0 is beautiful?
TOK: Mathematics and the knower. To what extent should mathematical knowledge be consistent with our intuition?
TOK: Nature of mathematics and science. What are the different meanings of induction in mathematics and science?
TOK: Knowledge claims in mathematics. Do proofs provide us with completely certain knowledge?
TOK: Knowledge communities. Who judges the validity of a proof?
TOK: Reason and mathematics. What is mathematical reasoning and what role does proof play in this form of reasoning? Are there
examples of proof that are not mathematical?
TOK: Mathematics, sense, perception and reason. If we can find solutions in higher dimensions, can we reason that these spaces
exist beyond our sense perception?
Are the Constants of Nature Really Constant? Article
A Mathematical Look at Fibonacci Numbers in nature Website
Daniel Tammet - The Boy With The Incredible Brain Video
The Fourth Dimension Article
The Tenth Dimension Video
Topic 2 - Functions
TOK: The nature of mathematics. Is mathematics simply the manipulation of symbols under a set of formal rules?
TOK: Mathematics and knowledge claims. Does studying the graph of a function contain the same level of mathematical rigour as
studying the function algebraically (analytically)?
Joel Cohen: An Introduction to Demography Video
How Folding Paper Can Get You to the Moon. Video
Topic 3 - Trigonometry
TOK: Mathematics and the knower. Why do we use radians? (The arbitrary nature of degree measure versus radians as real
numbers and the implications of using these two measures on the shape of sinusoidal graphs.)
TOK: Mathematics and knowledge claims. If trigonometry is based on right triangles, how can we sensibly consider trigonometric
ratios of angles greater than a right angle?
TOK: Mathematics and the world. Music can be expressed using mathematics. Does this mean that music is mathematical, that
mathematics is musical or that both are reflections of a common “truth”?
TOK: Mathematics and knowledge claims. How can there be an infinite number of discrete solutions to an equation?
TOK: Nature of mathematics. If the angles of a triangle can add up to less than 180°, 180° or more than 180°, what does this tell us
about the “fact” of the angle sum of a triangle and about the nature of mathematical knowledge?
Donald Duck in Math Magic Land - Pythagoras and Music
Babylonian Numerals Website
Mathematics and Music Articles
Non-Euclidean Geometry Website
Topic 4 - Vectors
TOK: Mathematics and knowledge claims. You can perform some proofs using different mathematical concepts. What does this tell
us about mathematical knowledge?
TOK: The nature of mathematics. Why this definition of scalar product?
TOK: The nature of mathematics. Why might it be argued that vector representation of lines is superior to Cartesian?
TOK: Mathematics and the knower. Why are symbolic representations of three-dimensional objects easier to deal with than visual
representations? What does this tell us about our knowledge of mathematics in other dimensions?
Relating Relativity Article
Face to Face Article
Topic 5 - Statistics & Probability
TOK: The nature of mathematics. Why have mathematics and statistics sometimes been treated as separate subjects?
TOK: The nature of knowing. Is there a difference between information and data?
TOK: Mathematics and knowledge claims. Is independence as defined in probabilistic terms the same as that found in normal
experience?
TOK: Mathematics and the knower. To what extent can we trust samples of data?
TOK: Mathematics and the real world. Is the binomial distribution ever a useful model for an actual real-world situation?
TOK: Mathematics and knowledge claims. To what extent can we trust mathematical models such as the normal distribution?
Double Slit Experiment Video
Peter Donnelly: How Stats Fool Juries Video
Prior Probability: The Dirty Little Secret of “Evidence- Based Alternative Medicine”
The Meaning of Life??? Possible Simulation Theory
Derren Brown - Coin Toss
The Drugs Don't Work: A Modern Medical Scandal
Go to Article
Online ESP test – test ESP claims using binomial
model.On-Line Test
Topic 6 - Calculus
TOK: The nature of mathematics. Does the fact that Leibniz and Newton came across the calculus at similar times support the
argument that mathematics exists prior to its discovery?
TOK: Mathematics and the knower. What does the dispute between Newton and Leibniz tell us about human emotion and
mathematical discovery?
TOK: Mathematics and knowledge claims. Euler was able to make important advances in mathematical analysis before calculus
had been put on a solid theoretical foundation by Cauchy and others. However, some work was not possible until after
Cauchy’s work. What does this tell us about the importance of proof and the nature of mathematics?
TOK: Mathematics and the real world. The seemingly abstract concept of calculus allows us to create mathematical models that
permit human feats, such as getting a man on the Moon. What does this tell us about the links between mathematical models
and physical reality?
A Brief History of Infinity: Space Video
Mandelbrot - The Secret Life of Chaos Video
What is Time? Article
Gabriel's Horn Article
Topic 1 - Algebra
TOK: Mathematics and the world. Some mathematical constants (pi, e, , Fibonacci numbers) appear consistently in nature. What does this tell us about mathematical knowledge?
TOK: Mathematics and the knower. How is mathematical intuition used as a basis for formal proof? (Gauss’ method for adding up
integers from 1 to 100.)
TOK: The nature of mathematics and science. Were logarithms an invention or discovery?
TOK: The nature of mathematics. The unforeseen links between Pascal’s triangle, counting methods and the coefficients of
polynomials. Is there an underlying truth that can be found linking these?
TOK: Mathematics and the knower. Do the words imaginary and complex make the concepts more difficult than if they had
different names?
TOK: The nature of mathematics. Has “i” been invented or was it discovered?
TOK: Mathematics and the world. Why does “i” appear in so many fundamental laws of physics?
TOK: The nature of mathematics. Was the complex plane already there before it was used to represent complex numbers
geometrically?
TOK: Mathematics and the knower. Why might it be said that e^ip + 1 = 0 is beautiful?
TOK: Mathematics and the knower. To what extent should mathematical knowledge be consistent with our intuition?
TOK: Nature of mathematics and science. What are the different meanings of induction in mathematics and science?
TOK: Knowledge claims in mathematics. Do proofs provide us with completely certain knowledge?
TOK: Knowledge communities. Who judges the validity of a proof?
TOK: Reason and mathematics. What is mathematical reasoning and what role does proof play in this form of reasoning? Are there
examples of proof that are not mathematical?
TOK: Mathematics, sense, perception and reason. If we can find solutions in higher dimensions, can we reason that these spaces
exist beyond our sense perception?
Are the Constants of Nature Really Constant? Article
A Mathematical Look at Fibonacci Numbers in nature Website
Daniel Tammet - The Boy With The Incredible Brain Video
The Fourth Dimension Article
The Tenth Dimension Video
Topic 2 - Functions
TOK: The nature of mathematics. Is mathematics simply the manipulation of symbols under a set of formal rules?
TOK: Mathematics and knowledge claims. Does studying the graph of a function contain the same level of mathematical rigour as
studying the function algebraically (analytically)?
Joel Cohen: An Introduction to Demography Video
How Folding Paper Can Get You to the Moon. Video
Topic 3 - Trigonometry
TOK: Mathematics and the knower. Why do we use radians? (The arbitrary nature of degree measure versus radians as real
numbers and the implications of using these two measures on the shape of sinusoidal graphs.)
TOK: Mathematics and knowledge claims. If trigonometry is based on right triangles, how can we sensibly consider trigonometric
ratios of angles greater than a right angle?
TOK: Mathematics and the world. Music can be expressed using mathematics. Does this mean that music is mathematical, that
mathematics is musical or that both are reflections of a common “truth”?
TOK: Mathematics and knowledge claims. How can there be an infinite number of discrete solutions to an equation?
TOK: Nature of mathematics. If the angles of a triangle can add up to less than 180°, 180° or more than 180°, what does this tell us
about the “fact” of the angle sum of a triangle and about the nature of mathematical knowledge?
Donald Duck in Math Magic Land - Pythagoras and Music
Babylonian Numerals Website
Mathematics and Music Articles
Non-Euclidean Geometry Website
Topic 4 - Vectors
TOK: Mathematics and knowledge claims. You can perform some proofs using different mathematical concepts. What does this tell
us about mathematical knowledge?
TOK: The nature of mathematics. Why this definition of scalar product?
TOK: The nature of mathematics. Why might it be argued that vector representation of lines is superior to Cartesian?
TOK: Mathematics and the knower. Why are symbolic representations of three-dimensional objects easier to deal with than visual
representations? What does this tell us about our knowledge of mathematics in other dimensions?
Relating Relativity Article
Face to Face Article
Topic 5 - Statistics & Probability
TOK: The nature of mathematics. Why have mathematics and statistics sometimes been treated as separate subjects?
TOK: The nature of knowing. Is there a difference between information and data?
TOK: Mathematics and knowledge claims. Is independence as defined in probabilistic terms the same as that found in normal
experience?
TOK: Mathematics and the knower. To what extent can we trust samples of data?
TOK: Mathematics and the real world. Is the binomial distribution ever a useful model for an actual real-world situation?
TOK: Mathematics and knowledge claims. To what extent can we trust mathematical models such as the normal distribution?
Double Slit Experiment Video
Peter Donnelly: How Stats Fool Juries Video
Prior Probability: The Dirty Little Secret of “Evidence- Based Alternative Medicine”
The Meaning of Life??? Possible Simulation Theory
Derren Brown - Coin Toss
The Drugs Don't Work: A Modern Medical Scandal
Go to Article
Online ESP test – test ESP claims using binomial
model.On-Line Test
Topic 6 - Calculus
TOK: The nature of mathematics. Does the fact that Leibniz and Newton came across the calculus at similar times support the
argument that mathematics exists prior to its discovery?
TOK: Mathematics and the knower. What does the dispute between Newton and Leibniz tell us about human emotion and
mathematical discovery?
TOK: Mathematics and knowledge claims. Euler was able to make important advances in mathematical analysis before calculus
had been put on a solid theoretical foundation by Cauchy and others. However, some work was not possible until after
Cauchy’s work. What does this tell us about the importance of proof and the nature of mathematics?
TOK: Mathematics and the real world. The seemingly abstract concept of calculus allows us to create mathematical models that
permit human feats, such as getting a man on the Moon. What does this tell us about the links between mathematical models
and physical reality?
A Brief History of Infinity: Space Video
Mandelbrot - The Secret Life of Chaos Video
What is Time? Article
Gabriel's Horn Article
Cross Curricular Links
|
|
|
|